Ο Γκάους στη ζωή μας…



Ο Καρλ Φρίντριχ Γκάους ήταν Γερμανός μαθηματικός που γεννήθηκε το 1777 στην Μπράουνσβαϊγκ της Γερμανίας και πέθανε το 1855 στο Γκέτινγκεν.
Θεωρείται ως ο «μεγαλύτερος Μαθηματικός μετά τον Αρχιμήδη και τον Ευκλείδη». Ονομάστηκε ο «πρίγκιπας των Μαθηματικών» και ένας από τους δυο μεγαλύτερους Γερμανούς Μαθηματικούς όλων των εποχών. Ήδη σε ηλικία 18 ετών ανέπτυξε τη θεωρία των συναρτήσεων κατανομής, και στη συνέχεια του βίου του προσέφερε ερευνητικά σε πολλά επιστημονικά πεδία. Στη θεωρία των αριθμών, τη μαθηματική ανάλυση, τη στατιστική, τη διαφορική γεωμετρία, τη μη-Ευκλείδεια γεωμετρία, τη γεωδαισία, την ηλεκτροστατική, την οπτική, τον γεωμαγνητισμό και πολλά άλλα. Από κάποιους, του αποδόθηκε ο χαρακτηρισμός homouniversalis, τιμητικός χαρακτηρισμός καθολικής ευρυμάθειας σε επιστήμη και τέχνες, που έχει αποδοθεί μόνο στον Αριστοτέλη, τον Νεύτωνα, τον Λάιμπνιτς και πιθανόν ισχύει μόνο για τον Λεονάρντο ντα Βίντσι.
Η ευρύτερα γνωστή μαθηματική σχέση του Γκάους είναι η της «κανονικής κατανομής» που δίδεται με τη μαθηματική σχέση:
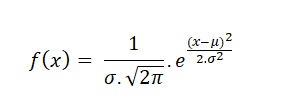
(Έντρομε αναγνώστη μπορείς να συνεχίσεις την ανάγνωση. Δεν υπάρχουν άλλες δυσνόητες μαθηματικές σχέσεις!).
Ανάλογα με την επιλογή των σταθερών μ και σ η μαθηματική σχέση παρίσταται γραφικά όπως φαίνεται στο παρακάτω γράφημα.
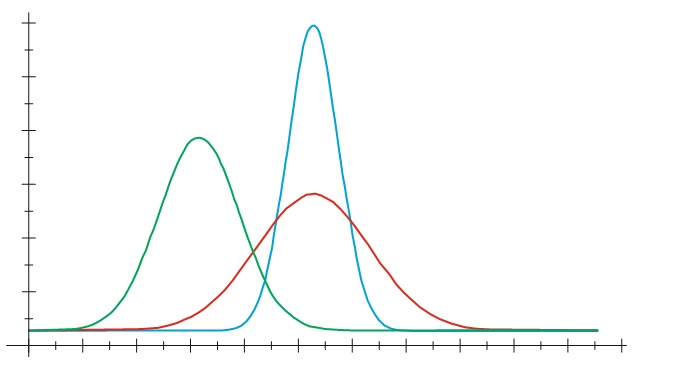
Σε κάθε περίπτωση η γραφική παράσταση έχει τη μορφή καμπάνας και γι’ αυτό έγινε γνωστή ως «κωδωνοειδής καμπύλη» (Αγγλικά: bellcurve, Γερμανικά: Glockenkurve κ.λπ.). Η «κανονική κατανομή» είναι η σπουδαιότερη από τις διάφορες κατανομές, ιδιαίτερα σημαντική στη στατιστική και χρησιμοποιείται συχνότατα στις φυσικές και κοινωνικές επιστήμες για να αποδώσει τυχαίες μεταβλητές πραγματικής αξίας, των οποίων οι κατανομές είναι άγνωστες. Φαινόμενα που ακολουθούν την κανονική κατανομή - χαρακτηριστικά αναφέρω - την ταχύτητα των μορίων στα ιδανικά αέρια, το αποτέλεσμα μέτρησης IQ μιας ομάδας ατόμων, το ύψος των μαθητών μιας τάξης, το βάρος των δεκαοχτάχρονων μαθητριών, οι ετήσιες πωλήσεις μιας εταιρείας κινητών τηλεφώνων, η απόκλιση στο βάρος εμφιαλωμένου νερού, ο χρόνος λειτουργίας ενός είδους λαμπτήρων, ο ρυθμός ανθοφορίας της πορτοκαλιάς ή της λεμονιάς στον κήπο μας και μη αριθμήσιμες άλλες περιπτώσεις.
Επεξηγηματικά, η καμπύλη της «κανονικής κατανομής» υποδεικνύει ότι, ένα μετρήσιμο μέγεθος παρουσιάζει αυξημένη πυκνότητα σε κάποιο σημείο, περίπου στο κέντρο και μειώνεται σταδιακά και σχεδόν συμμετρικά προς τις δυο πλευρές, μέχρι μηδενισμού. Εάν π.χ. μετρήσουμε το ύψος των 17χρονων κοριτσιών μιας χώρας, περίπου στα 1,60 μέτρα η πυκνότητα (δηλαδή το ποσοστό κοριτσιών με αυτό το ύψος) θα μεγιστοποιείται και σταδιακά το ποσοστό θα φθίνει, τείνοντας προς το μηδέν αμφίπλευρα, αφού δίμετρα άτομα ή νάνοι σπανίζουν.
Η θεωρία της «κανονικής κατανομής» έχει τη βάση της σε ένα ισχυρό αποτέλεσμα της Θεωρίας των Πιθανοτήτων που πρώτος διατύπωσε το 1733 ο Γάλλος μαθηματικός Abrahamde Moivre,το «Κεντρικό Οριακό Θεώρημα» και αργότερα συνέχισε θεωρητικά ο Γάλλος μαθηματικός Laplace. Στη θεωρητικές βάσεις των μεγάλων Γάλλων μαθηματικών, διατυπώνει ο Γκάους την θεωρία της «κανονικής κατανομής» και επαληθεύει για πρώτη φορά πειραματικά. Αρχικά διαπίστωσε ότι τα σφάλματα που υπόκεινται οι αστρονομικές παρατηρήσεις περιγράφονται ικανοποιητικά από την κανονική κατανομή. Στη συνέχεια διαπίστωσε ότι, γενικότερα, τα τυχαία, μη συστηματικά σφάλματα, προσεγγίζονται με ακρίβεια από την κανονική κατανομή. Σε ένδειξη ευγνωμοσύνης, της μεγάλης συνεισφοράς του Γκάους στην ανάδειξη των ιδιοτήτων και της σημασίας της, η «κανονική κατανομή» ονομάζεται και «κατανομή Γκάους» (ενίοτε και Gauß-Laplace).
Προσωπικά δεν γνωρίζω καμία σύνθετη μαθηματική σχέση με τόσο ευρεία πρακτική εφαρμογή. Συγκρίσιμη, κατά την άποψή μου, μόνο με τη γεωμετρική σχέση της χρυσής τομής των αρχαίων Ελλήνων. Η μία, παρουσιάζεται σε αμέτρητα παραδείγματα της εφαρμοσμένης στατιστικής και, η άλλη, καθορίζει την αισθητική μας ισορροπία, στη φύση, στην αρχιτεκτονική, στην τέχνη.
Επίκαιρο παράδειγμα «κανονικής κατανομής» είναι το ιστόγραμμα, των μολυσμένων από κορωνοϊό με ηλικιακή κατάταξη, όπως παρουσιάζεται από τον ΕΟΔΥ.
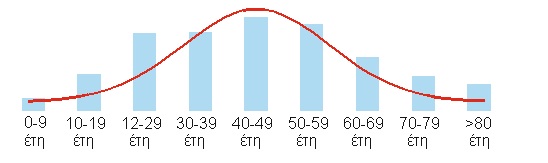
Όσο μεγαλύτερο είναι το αντιπροσωπευτικό δείγμα τόσο περισσότερο πλησιάζει το ιστόγραμμα την κωδωνοειδή καμπύλη.
Σκανδαλισμό, για να επαναφέρω στη μνήμη μου τον Γκάους και την κωδωνοειδή καμπύλη του, μετά από 55 χρόνια απουσίας από τα φοιτητικά θρανία, ήταν το τρανταχτό γέλιο φίλου μου γιατρού, όταν του γνωστοποίησα την πρόθεσή μου, πριν τον εμβολιασμό μου για COVID-19, να κάνω εξέταση αντισωμάτων, μήπως ανήκω στην ευτυχή ομάδα ασυμπτωματικών και επομένως δεν είναι αναγκαίος ο εμβολιασμός μου. Αποφάσισα, λοιπόν, να υπολογίσω χονδρικά, σύμφωνα με την κανονική κατανομή, τις πιθανότητες ογδοντάχρονων ατόμων, να είναι ασυμπτωματικοί στον COVID-19,με στοιχεία μετρήσεων που συνέλεξα από το ιντερνέτ. Αυτονόητα, έθεσα οριακές τιμές το μηδέν έτος, με (σχεδόν) 100% ασυμπτωματικά άτομα (βρέφη), και τα εκατοστό έτος με (σχεδόν) 0% ασυμπτωματικούς (υπερήλικες). Τα αποτελέσματα των πρόχειρων υπολογισμών μου απεικονίζονται στην παρακάτω ημικωδωνοειδή καμπύλη.
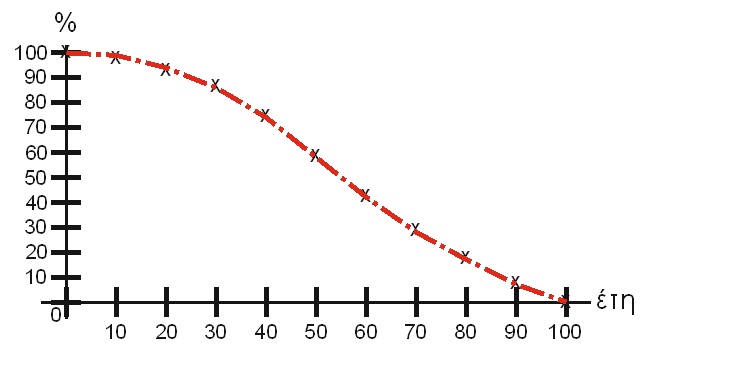
Όπως φαίνεται από το διάγραμμα, άτομα ηλικίας ογδόντα ετών έχουν περίπου 20% πιθανότητα να είναι ασυμπωματικά. Η τιμή αυτή αποτελεί το μέσο όρο. Για εξατομίκευση του μέσου όρου μιας ηλικιακής ομάδας (π.χ. των ογδοντάρηδων) του παραπάνω διαγράμματος, θα ήταν αναγκαία η περαιτέρω διερεύνηση, και πάλι μέσω της κανονικής κατανομής, βασιζόμενοι στην φυσιολογική κατάσταση και στην ανταπόκριση του ανοσοποιητικού συστήματος σε ιογενείς εισβολείς, της εξεταζόμενης ομάδας. Κάτι τέτοιο είναι ανέφικτο, λόγω έλλειψης (εξατομικευμένων) στοιχείων. Με βεβαιότητα όμως ισχυρίζομαι, βάσει και της εμπειρίας που αποκόμισα, ότι ένα ικανοποιητικό ποσοστό ογδοντάρηδων, έχει πιθανότητα 50% να είναι ασυμπτωματικό. Παρ’ όλο που στον υπολογισμό της κατανομής Γκάους δεν τηρήθηκαν (για ευνόητους λόγους) αυστηρά οι κανόνες της μαθηματικής δεοντολογίας, ισχυρίζομαι με βεβαιότητα ότι, τα αποτελέσματα είναι χωρίς μεγάλες αποκλίσεις και επομένως στατιστικά αποδεκτά. Άρα, η πρόθεσή μου να εξετάσω το επίπεδο αντισωμάτων στον κορωνοϊό, πριν εμβολιασθώ, ούτε υπεραισιόδοξη ήταν, και σε καμία περίπτωση, σύμφωνα με τη στατιστική, εξωπραγματική.
Στο ερώτημα εάν θα έπρεπε με αυτό τον τρόπο να γίνει η διαχείριση των εμβολιασμών, δηλαδή να γίνει πρώτα έλεγχος αντισωμάτων και εξαίρεση από τον εμβολιασμό των ασυμπτωματικών, με μαθηματική βεβαιότητα ισχυρίζομαι ότι κάτι τέτοιο θα ήταν ανέφικτο. Οργανωτικός σχεδιασμός, επιχειρησιακός συντονισμός, κόστος εφαρμογής, χρόνος εκτέλεσης, και άλλοι παράγοντες καθιστούν ένα τέτοια εγχείρημα ανεφάρμοστο. Δυστυχώς η μόνη δυνατότητα για ταχεία επίτευξη της ποθητής ελευθερώτριας ανοσίας της αγέλης (ή της κοινότητας αν το επιθυμείτε) είναι ή η απόλυτη ελευθερία κίνησης, χωρίς περιορισμούς, με εκατόμβες νεκρών και τεράστιο κοινωνικό κόστος ή ο ταχύς καθολικός εμβολιασμός της κοινότητας με ασφαλή και αποτελεσματικά εμβόλια. Τα εμβόλια που χρησιμοποιούνται σήμερα, και αναπτύχθηκαν πράγματι σε ρεκόρ χρόνου, αποδείχθηκαν βραχυπρόθεσμα ασφαλή και αποτελεσματικά. Επειδή η περίοδος παρακολούθησης είναι σχετικά πολύ μικρή, αν είναι πράγματι καθολικά ασφαλή και αποτελεσματικά για εύλογο χρονικό διάστημα, διαψεύδοντας τους πολέμιούς τους, θα δείξει ο χρόνος. Σε κάθε περίπτωση θεωρώ κοινωνικό μας καθήκον, εφόσον αυτή είναι η παγκόσμια επιλογή, τον έστω ακούσιο εμβολιασμό μας. Επίσης θεωρώ, επιεικώς εκφραζόμενος, αντικοινωνική και απαράδεκτη την αρνητική στάση ορισμένων υγειονομικών στον εμβολιασμό, που βρίσκεται σε πλήρη αναντιστοιχία με την παγκοσμίως αναγνωρισμένη τεράστια προσφορά των συναδέλφων τους. Υπάρχει βέβαια και η Κινέζικη Μέθοδος διαχείρισης της πανδημίας, ανεφάρμοστη όμως στους δημοκρατικά ευαίσθητους (ή σύμφωνα με άλλους απείθαρχους και επομένως κοινωνικά αναίσθητους) λαούς της δύσης.
Μεγάλος αριθμός στατιστικολόγων, δημοσκόπων, λοιμωξιολόγων, ερευνητών βιοστατιστικής και επιδημιολογίας και άλλων επιστημόνων χρησιμοποιούν τις στατιστικές μεθόδους και ιδιαίτερα την συνάρτηση της «κανονικής κατανομής»του Γκάους, και όπως αυτή διαμορφώθηκε και διευρύνθηκε από επόμενους στατιστικολόγους. Όμως η συντριπτική πλειοψηφία, σήμερα πλέον με την επικράτηση των PC, ακούσια, χωρίς ούτε καν να γνωρίζει το όνομα του Γκάους. Περίτεχνα υπολογιστικά προγράμματα, στα οποία ο χρήστης πρέπει να εισάγει μόνο κάποιες σταθερές παραμέτρους, επιλύουν σε δέκατα του δευτερολέπτου τη δυσνόητη και πολύπλοκη εξίσωση, και τις άλλες που ακολούθησαν. Οι μαθηματικές σχέσεις, αγνώριστα μασκαρεμένες με bit και Byte μεταφέρονται με ταχύτητα φωτός μεταξύ RAM, ROM και CPU και παρουσιάζονται, πριν ολοκληρωθεί το κλικ στο ποντίκι, στο Μόνιτορ του υπολογιστή. Έμαθα, τα τελευταία χρόνια με την επικράτηση των προσωπικών υπολογιστών, να χειρίζομαι περισσότερα από δέκα σχεδιαστικά και υπολογιστικά προγράμματα. Ένα ελαφρό πάτημα πλήκτρου και χιλιάδες πράξεις, πολλές φορές εκατομμύρια, εκτελούνται. Η εργασία ημερών ή εβδομάδων του παρελθόντος, της φοιτητικής μου περιόδου, εκτελείται αλάνθαστα σε δέκατα δευτερολέπτου. Σε κανένα από αυτά τα προγράμματα δεν γνωρίζω ποια αλγεβρική ή γεωμετρική σχέση ή ποια διανυσματικά μεγέθη υπολογίζονται για την παρουσίαση της λύσης στη οθόνη. Όμως η ομορφιά, ο ρομαντισμός η προσωπική επαφή με τις μαθηματικές σχέσεις (στην προκειμένη περίπτωση του Γκάους) χάθηκε. Ρομαντισμός σε μια μαθηματική σχέση; Τι σουρεαλισμός! Ιερόσυλα παραφράζοντας τον Γαλιλαίο θα ισχυριστώ «και όμως (κινείται!) …ισχύει!)». Ήδη οι Πυθαγόρειοι το 500 π.Χ. συνέδεσαν τη μουσική με τα μαθηματικά. Τον λόγο των ακέραιων αριθμών με την αρμονία της μουσικής αλλά και του σύμπαντος. Αλλά και η αισθητική αρμονία εξαρτάται από την ισότητα «του μέσου προς άκρον λόγον» του Ευκλείδη ή της καθ’ ημάς «χρυσής τομής». Το ρομαντικό με το ορθολογικό, βαγόνια στις ίδιες ράγες. Ο καταθλιπτικός μαθηματικός Γκέντελ σε τι διαφέρει από το δαιμονισμένο ζωγράφο Μοντιλιάνι; Κι ο σχιζοφρενής μαθηματικός Νας απλώς δεν έκοψε το αυτί του, όπως ο Βαν Γκονγκ, και αναγνωρίστηκε, με Νόμπελ, πριν το θάνατό του. Καμιά άλλη διαφορά. Το αποδεικνύει ο πίνακας του Βαν Γκονγκ «στο Κατώφλι της Αιωνιότητας». Καμιά διαφορά μεταξύ τους στο ρομαντισμό, στο όραμα, στην αφοσίωση, στην αυταπάρνηση, στην πίστη, στην παράνοια, στο θάνατο. Και τα έργα τους συγκρίσιμα; Το θεώρημα της «Μη πληρότητας» του Γκέντελ σε σύγκριση με την «Jeanne» του Μοντιλιάνι; Και η «Ισορροπία Νας» συγκρίσιμη με το «Έναστρη Νύχτα» του Βαν Γκονγκ; Σουρεαλισμός; Αναίδεια; Παράνοια; ή Ρομαντική λογική; Αναγνώστη σε παρακαλώ, πριν δώσεις απαντήσεις στα παραπάνω ερωτήματα, απάντησε πρώτα: Στον πίνακα του «στο Κατώφλι της Αιωνιότητας» ο Βαν Γκονγκ ποιον απεικονίζει; Τον ίδιο; Τον καταθλιπτικό Γκέντελ, τον δαιμονισμένο Μοντιλιάνι ή τον σχιζοφρενή Νας; Μήπως και τους τέσσερις;

Στο Κατώφλι (Πύλη) της Αιωνιότητας (Βενσέντ βαν Γκονγκ)
Υπομονετικέ αναγνώστη! Αν έφτασες μέχρι το τέλος της διήγησής μου, πήρες, ως συνηθίζεται να λέγεται, την άχρηστη πληροφορία. Πως, ένας μεγάλος Γερμανός Μαθηματικός, μπήκε, με δυσάρεστο τρόπο, ακούσια στην καθημερινότητα μας.
















